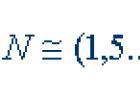Информационная коррекция переменных систематических погрешностей средств измерений и измерительных информационных систем
Рецензент:
Туз Ю.М.
директор НИИ АЭИ, д.т.н., проф., лауреат Государственной премии Украины в области науки и техники
Вступление
Требования к точности, правильности и сходимости средств измерений постоянно возрастают. Повышение требований обычно проводилось путем перехода от используемого к новому физическому принципу измерения, который и обеспечивал более высокие качества измерений. Одновременно совершенствовались методика и техника проведения измерений, ужесточались требования к комплексу нормальных (стандартных) условий, сопровождающих процесс измерений.
Любые измерительные прибор, система, канал «реагируют» не только на измеряемую величину, но и на внешнюю среду, т.к. неизбежно связаны с нею.
Хорошей иллюстрацией этого теоретического тезиса может быть влияние приливных волн, вызванных Луной в земной коре, на изменение энергии заряженных частиц, полученных на большом кольцевом ускорителе в Центре европейских ядерных исследований. Приливная волна деформирует 27-километровое (2,7·10 7 мм) кольцо ускорителя и изменяет длину пробега частиц по кольцу приблизительно на 1 мм (!). Это приводит к изменению энергии ускоренной частицы почти на десять миллионов электронвольт. Указанные изменения очень малы, но превышают возможную погрешность измерений примерно в десять раз и уже привели к серьезной ошибке в измерении массы бозона.
Постановка проблемы
Метрологическое обеспечение радиоэлектронных измерений может быть охарактеризовано следующей типичной проблематикой . Использование теоретических методов анализа влияния факторов внешней среды на погрешности средств измерений затруднительно. Характер влияния сложен, нестабилен, трудно интерпретируем с позиций логически-профессионального анализа специалистом; изменчив при переходе от экземпляра к экземпляру одного и того же типа средств измерений .
Отмечается методологическая сложность получения зависимостей неизвестного вида от нескольких переменных и то, что «...возможности исследования зависимостей погрешности от факторов внешней среды весьма ограничены и мало достоверны, особенно в отношении совместных влияний факторов и динамических изменений их значений» .
В результате приведенных причин и значительного разнообразия их проявления делается вывод, что для группы средств измерений одного типа наиболее адекватным описанием погрешностей средств измерений от влияющих факторов внешней среды следует признать зону неопределенности, границы которой определяются крайними зависимостями экземпляров .
Указанные трудности в решении проблемы уменьшения погрешностей средств измерений есть следствие системных свойств этих средств: эмергентности, целостности, неопределенности, сложности, стохастичности и др. . Попытки теоретического описания на уровне номографических наук в рассматриваемых ситуациях часто не эффективны. Необходим экспериментально-статистический подход, т. к. он позволяет провести идиографическое описание закономерности конкретных явлений в детальных условиях времени и места .
Как в радиоэлектронных измерениях , так и в обеспечении точности оценивания результатов количественного химического анализа отмечается важная особенность погрешностей: систематические погрешности результата для большинства средств измерений существенны в том смысле, что они превышают случайную, и погрешность данного экземпляра средства измерения в каждой точке факторного пространства определяется, в основном, постоянной величиной.
Для дальнейшего повышения качества проводимых измерений необходимо использовать не только физические – конструкторские, технологические, эксплуатационные – возможности, но и информационные. Они заключаются в реализации системного подхода в получении информации о всех видах погрешностей: инструментальных, методических, дополнительных, систематических, прогрессирующих (дрейфовых), модельных и возможно др. Имея такую информацию в виде многофакторной математической модели и зная значения факторов (условий), сопровождающих процесс измерения, можно получить информацию о приведенных погрешностях и, следовательно, более точно знать измеряемую величину.
Требования к методологии математического моделирования систематических погрешностей средств измерений
Необходимо разработать методику многофакторного математического моделирования закономерно изменяющихся систематических погрешностей с учетом следующих требований.
- Системный подход к описанию систематических погрешностей с учетом множества факторов и, если необходимо, множества критериев качества средства измерения.
- Прикладной уровень получения математических моделей, когда их структура исследователю не известна.
- Эффективность (в статистическом смысле) получения полезной информации из исходных данных и отражение ее в математических моделях.
- Возможность доступной и удобной содержательной интерпретации полученных моделей в предметной области.
- Эффективность использования математических моделей в предметной области по сравнению с затратами ресурсов на их получение.
Основные этапы получения математических моделей
Рассмотрим основные этапы получения многофакторных математических моделей, соответствующих вышеприведенным требованиям.
Выбор плана многофакторного эксперимента, обеспечивающего необходимые свойства получаемых математических моделей
В рассматриваемом (метрологическом) классе проводимых экспериментальных исследований возможно использование полного и дробного факторного эксперимента. Под определяемой математической моделью будем понимать линейную относительно параметров и нелинейную в общем случае относительно факторов модель произвольно высокой, но конечной сложности. В расширенную матрицу эффектов полного факторного эксперимента будет входить столбец фиктивного фактора X 0 = 1, столбцы всех главных эффектов и всех возможных взаимодействий главных эффектов. Если эффекты факторов и взаимодействий факторов выразить в виде системы ортогональных нормированных контрастов, то матрица дисперсий-ковариаций примет вид:
где X
– матрица эффектов полного факторного эксперимента;
σ y 2 – дисперсия воспроизводимости результатов опытов;
N
– число опытов в плане эксперимента;
Е
– единичная матрица.
Математическая модель, полученная по схеме полного факторного эксперимента, соответствует многим замечательным свойствам: коэффициенты модели ортогональны друг другу и в статистическом смысле независимы; максимально устойчивы (cond = 1); каждый коэффициент несет семантическую информацию о влиянии соответствующего эффекта на моделируемый критерий качества; план эксперимента соответствует критериям D -, A -, E -, G -оптимальности, а также критерию пропорциональности частот уровней факторов; математическая модель адекватна в точках аппроксимации поверхности отклика . Будем считать такую модель истинной и «наилучшей».
В тех случаях, когда использование полного факторного эксперимента невозможно по причине большого числа опытов, следует рекомендовать применять многофакторные регулярные (желательно равномерные) планы экспериментов. При правильном выборе числа необходимых опытов их свойства максимально близки к приведенным свойствам полного факторного эксперимента .
Получение структуры многофакторной математической модели
Структуру получаемой многофакторной математической модели, в общем случае не известной исследователю, необходимо определять, исходя из возможного множества эффектов, соответствующих множеству эффектов схемы полного факторного эксперимента. Она задается выражением :
где X 1 ,..., X k – факторы искомой математической модели;
s 1 ,..., s k – число уровней факторов X 1 ,..., X k ;
k – общее число факторов;
N п – число опытов полного факторного эксперимента, равное числу структурных элементов его схемы.
Поиск необходимых эффектов – главных и взаимодействий – в виде ортогональных контрастов для искомой модели осуществляется как многократная статистическая проверка гипотез о статистической значимости эффектов. В модель вводят статистически значимые эффекты.
Выбор числа необходимых опытов для дробного факторного эксперимента
Обычно исследователю известна (приближенно) информация о предполагаемой сложности влияния факторов на моделируемый критерий качества. Для каждого фактора выбирается число уровней его варьирования, которое должно быть на 1 больше максимальной степени полинома, необходимой для адекватного описания этим фактором поверхности отклика. Необходимое число экспериментов будет :

где s i – число уровней фактора X i ; 1 ≤ i ≤ k .
Коэффициент 1,5 выбирается для случая, когда число необходимых экспериментов значительно (порядка 50...64 и более). При меньшем необходимом числе экспериментов следует выбирать коэффициент 2.
Выбор структуры многофакторной математической модели
Для выбора структуры получаемой математической модели необходимо использовать разработанный алгоритм . В алгоритме реализована последовательная схема выделения необходимой структуры по результатам спланированного многофакторного эксперимента.
Обработка результатов экспериментов
Для комплексной обработки результатов экспериментов и получения необходимой информации для интерпретации результатов в предметной области разработано программное средство «Планирование, регрессия и анализ моделей» (ПС ПРИАМ) . Разработчик – лаборатория экспериментально-статистических методов кафедры технологии машиностроения Национального технического университета Украины «Киевский политехнический институт». Оценка качества получаемых математических моделей включает следующие критерии:
- получение информативного подмножества главных эффектов и взаимодействий факторов для принятия в качестве структуры искомой многофакторной математической модели;
- обеспечение максимально высокой теоретической эффективности (вплоть до 100%) извлечения полезной информации из исходных данных;
- проверка на статистическую значимость потенциальной математической модели;
- проверки различных предпосылок множественного регрессионного анализа;
- проверка на адекватность полученной модели;
- проверка на информативность, т.е. присутствие в математической модели полезной информации и ее статистической значимости;
- проверка на устойчивость коэффициентов математической модели;
- проверка фактической эффективности извлечения полезной информации из исходных данных;
- оценка семантичности (информационной) по полученным коэффициентам математической модели;
- проверка свойств остатков;
- общая оценка свойств полученной математической модели и возможности ее использования для достижения поставленной цели.
Интерпретация полученных результатов
Осуществляется специалистом (или специалистами), хорошо понимающими как формальные результаты в полученных моделях, так и те прикладные цели, для достижения которых должны быть использованы модели.
Математический метод получения полезной информации о систематических погрешностях, сопровождающих процесс измерения физической величины, и средство измерения создают надсистему со взаимодействием (иначе эмергентностью) между собой. Эффект взаимодействия – более высокая точность измеряемой величины – принципиально нельзя получить только за счет отдельных подсистем. Это следует из структуры математической модели Ŷ (ŷ 1 ,..., ŷ p) = f j (СИ, ММ) для эксперимента 2 2 //4 (отсутствие подсистемы задается «–1», а присутствие «1») указанных подсистем:
где Ŷ (ŷ 1 ,..., ŷ p) – вектор эффективности функционирования средства измерения, 1 ≤ j ≤ p ;
1 – символ среднего значения результата (условное начало отсчета);
СИ – результат измерения, полученный только от средства измерения;
ММ – информация, полученная по многофакторной математической модели о систематических погрешностях используемого средства измерения при знании внутренних и внешних относительно его условий проведения замеров;
СИ · ММ – эффект взаимодействия (эмергентность) средства измерения и математической модели при условии их совместного использования.
Повышение точности измерения достигается за счет получения большего объема информации об условиях измерения и свойствах средства измерения во взаимодействии с внутренней и внешней относительно его средой.
Сочетание физических и информационных принципов на практике означает интеллектуализацию известных систем, в частности, создание интеллектуальных средств измерений. Объединение физических и информационных принципов в единую интегральную систему позволяет принципиально по-новому решать старые проблемы.
Пример повышения точности измерения цифровых весов
Рассмотрим возможности предложенного подхода на примере повышения точности цифровых весов с диапазоном взвешивания 0...100 кгс. Датчик весов емкостного типа с автономным питанием от переносного источника напряжения. Весы предназначены для эксплуатации в диапазоне температуры окружающей среды (воздуха) 0...60°С. Напряжение от автономного источника напряжения в процессе эксплуатации весов может изменяться в диапазоне 12,3...11,7 В при расчетном (номинальном) значении 12 В.
Предварительное исследование цифровых весов показало, что изменения температуры окружающей среды и питаемого напряжения в вышеприведенных диапазонах сравнительно мало влияют на показания емкостного датчика и, следовательно, на результаты взвешивания. Однако стабилизировать эти внешние и внутренние условия с необходимой точностью и поддерживать их в процессе функционирования весов не представлялось возможным ввиду того, что весы должны эксплуатироваться не в стационарных (лабораторных) условиях, а на борту перемещающегося объекта.
Исследование точности весов без учета влияния изменений температуры и питаемого напряжения показали, что средняя абсолютная погрешность аппроксимации составляет 0,16%, а среднеквадратичная погрешность остатка (в единицах измерения выходной величины взвешивания) равна 53,92.
Для получения многофакторной математической модели были приняты следующие обозначения факторов и значения их уровней.
X 1 – гистерезис. Уровни: 0 (нагрузка); 1 (разгрузка). Фактор качественный.
X 2 – температура окружающей среды. Уровни: 0; 22; 60°C.
X 4 – измеряемый вес. Уровни: 0; 20; 40; 60; 80; 100 кгс.
Учитывая принятые уровни варьирования факторов и сравнительно не трудоемкий объем испытаний было решено провести полный факторный эксперимент, т.е. 2 · 3 2 · 6//108. Исходные данные испытаний были предоставлены проф. П.В. Новицким. Каждый опыт был повторен только один раз, что нельзя признать хорошим решением. Желательно повторение каждого опыта два раза. Предварительный анализ исходных данных показал, что они со значительной вероятностью содержат грубые ошибки. Эти опыты были повторены и их результаты были исправлены.
Натуральные значения уровней варьирования факторов были преобразованы в ортогональные контрасты, иначе в систему ортогональных полиномов Чебышева.
С использованием системы ортогональных контрастов структура полного факторного эксперимента будет иметь следующий вид:
(1 + x 1) (1 + x 2 + z 2) (1 + x 3 + z 3) (1 + x 4 + z 4 + u 4 + v 4 + ω 4) → N 108
где x
1 ,..., x
4 ; z
2 ,..., z
4 ; u
4 , v
4 , ω 4 – соответственно линейные, квадратичные, кубический, четвертой и пятой степени контрасты факторов X
1 ,..., X
4 ;
N
108 – число структурных элементов для схемы полного факторного эксперимента.
Все эффекты (главные и взаимодействия) были нормированы
![]()
где x iu (p) – значение p -го ортогонального контраста i -го фактора для u-й строки матрицы планирования, 1 ≤ u ≤ 108, 1 ≤ p ≤ s i – 1; 1 ≤ i ≤ 4.
Предварительный расчет математической модели показал, что в качестве оценки дисперсии воспроизводимости может быть выбрана (приближенно) величина 20,1.
Число степеней свободы (условно) принято V 2 = 108.
Дисперсия была использована для определения стандартной ошибки коэффициентов уравнения регрессии.
Вычисление математической модели и всех ее критериев качества было проведено с использованием ПС ПРИАМ. Полученная математическая модель имеет вид
| ŷ = 28968,9 – 3715,13x 4 + 45,2083x 3 – 37,5229z 2 + 23,1658x 2 – 19,0708z 4 – 19,6574z 3 – 9,0094x 2 z 3 – 9,27434z 2 x 4 + 1,43465x 1 x 2 + 1,65431z 2 x 3 , | (2) |
x 1 = 2 (X 1 – 0,5);
x 2 = 0,0306122 (X 2 – 27,3333);
z 2 = 1,96006 (x 2 2 – 0,237337x 2 – 0,575594);
x 3 = 3.33333 (X 3 – 12);
z 3 = 1,5 (x 2 3 – 0,666667);
x 4 = 0,02 (X 4 – 50);
z 4 = 1,875 (x 2 4 – 0,466667);
u 4 = 3,72024 (x 3 4 – 0,808x 4);
v 4 = 7,59549 (x 4 4 – 1,08571x 2 4 + 0,1296).
Таблица 1
Критерии качества полученной математической модели
| Анализ адекватности модели | |
| Остаточная дисперсия | 21,1084 |
| Дисперсия воспроизводимости | 20,1 |
| Расчетное значение F -критерия | 1,05017 |
| Уровень значимости F -критерия для адекватности 0,05 для степеней свободы V 1 = 97; V 2 = 108 | |
| Табличное значение F -критерия для адекватности | 1,3844 |
| Табличное значение F -критерия (при отсутствии повторных опытов) | 1,02681 |
| Стандартная ошибка оценки | 4,59439 |
| Скоррект. с учетом степеней свободы | 4,80072 |
| Модель | адекватна |
| Прим.: Дисперсия воспроизводимости задана пользователем |
|
| Анализ информативности модели | |
| Доля рассеивания объясняемая моделью | 0,999997 |
| Введено регрессоров (эффектов) | 11 |
| Коэффициент множественной корреляции | 0,999999 |
| (скоррект. с учетом степеней свободы) | 0,999998 |
| F отношение для R | 3,29697·10 6 |
| Уровень значимости F -критерия для информативности 0,01 для степеней свободы V 1 = 10; V 2 = 97 | |
| Табличное значение F -критерия для информативности | 2,50915 |
| Мoдель | информативна |
| Критерий Бокса и Веца для информативности | больше 49 |
| Информативность модели | очень высокая |
Таблица 2
Статистические характеристики коэффициентов регрессии
| Наименование главного эффекта или взаимодействия главных эффектов | Коэффициент регрессии | Стандартная ошибка коэффициента регрессии | Вычисленное значение t -крит. | Доля участия в объяснении разброса моделируемой величины |
| x 4 | b 1 = –3715,13 | 0,431406 | 5882,9 | 0,999557 |
| x 3 | b 2 = 45,2083 | 0,431406 | 85,5631 | 0,000211445 |
| z 2 | b 3 = –37,5229 | 0,431406 | 62,2275 | 0,000111838 |
| x 2 | b 4 = 23,1658 | 0,431406 | 40,7398 | 4,79362·10 –5 |
| z 4 | b 5 = –19,0708 | 0,431406 | 33,0808 | 3,16065·10 –5 |
| z 3 | b 6 = –19,6574 | 0,431406 | 32,22 | 2,9983·10 –5 |
| x 2 z 3 | b 7 = –9,0094 | 0,431406 | 11,2035 | 3,62519·10 –6 |
| z 2 x 4 | b 8 = –9,27434 | 0,431406 | 10,5069 | 3,18838·10 –6 |
| x 1 x 2 | b 9 = 1,43465 | 0,431406 | 2,523 | 1,83848·10 –7 |
| z 2 x 3 | b 10 = 1,65431 | 0,431406 | 2,24004 | 1,44923·10 –7 |
b
0 = 28968,9
Уровень значимости для t
-критерия – 0,05
Для степеней свободы V
1 = 108. Табличное значение t
-критерия – 1,9821
В табл. 1 приведена распечатка критериев качества полученной многофакторной математической модели. Модель адекватна. Доля рассеивания, объясняемая моделью, весьма высока, т. к. модель высокоточная, изменчивость функции отклика велика, а ее случайная изменчивость сравнительно мала. Коэффициент множественной корреляции R весьма близок к 1 и устойчив, т. к. будучи скорректированным с учетом степеней свободы, практически не меняется. Статистическая значимость R весьма велика, т.е. модель очень информативна. Высокая информативность модели подтверждается также значением критерия Бокса и Веца. Коэффициенты модели максимально устойчивы: число обусловленности cond = 1. Полученная модель семантична в информационном смысле, т. к. все ее коэффициенты ортонормированны: они статистически независимы и могут сравниваться по абсолютной величине друг с другом. Знак коэффициента показывает характер влияния, а его абсолютная величина – силу влияния. Полученная модель наиболее удобна для интерпретации в предметной области.
Учитывая семантичные свойства полученной математической модели и доли участия каждого из эффектов модели в общей доле рассеивания, объясняемой моделью, можно провести содержательный информационный анализ формирования результата измерения исследуемых цифровых весов.
Превалирующая доля участия в результатах моделирования, равная 0,999557, создается линейным главным эффектом x 4 (с коэффициентом b 1 = –3715,13), т.е. измеряемым весом (табл. 2). Нелинейность z 4 (с коэффициентом b 5 = –19,07) сравнительно мала (3,16·10 –5) и ее учет в модели повышает точность измерения. Линейный эффект x 4 сравнительно слабо (3,19·10 –6) взаимодействует с квадратичным эффектом z 2 температуры окружающей среды: взаимодействие z 2 x 4 (b 8 = –9,27). Следовательно, математическая модель только от фактора измеряемый вес X 4 должна включать и эффект влияния температуры окружающей среды
ŷ 1 = 28968,90 – 3715,13x 4 – 19,07z 4 – 9,27z 2 x 4 ,
фактор которого X 2 является неуправляемым.
Напряжение питания изменяет результаты взвешивания в виде линейного эффекта x 3 (b 2 = 45,21) и квадратичного эффекта z 3 (b 6 = –19,66). Их суммарная доля участия составляет 2,41·10 –4 .
Температура окружающей среды влияет в виде квадратичного z 2 (b 3 = –37,52) и линейного x 2 (b 4 = 23,17) эффектов с суммарной долей участия 1,60·10 –4 .
Температура окружающей среды и напряжение питания образуют парное взаимодействие x 2 z 3 (b 7 = –9,01) c долей участия 3,63·10 –6 .
Доказательность статистической значимости двух последних эффектов x 1 x 2 и z 2 x 3 не может быть обоснована, т. к. они существенно меньше эффектов x 2 z 3 и z 2 x 4 , а обоснованное значение дисперсии воспроизводимости по результатам повторных опытов в представленных исходных данных, к сожалению, отсутствовало.
В табл. 2 приведены статистические характеристики коэффициентов регрессии. Отметим, что значения коэффициентов регрессии разделены на нормировочные коэффициенты ортогональных контрастов, которые не включены в приведенные формулы ортогональных контрастов. Этим и объясняется то, что при делении значений коэффициентов регрессии на их стандартную ошибку полученные значения t -критерия отличаются от приведенных правильно вычисленных значений этого критерия в табл. 2.

Рис. 1. Гистограмма остатков
На рис. 1 показана гистограмма остатков ![]() . Она сравнительно близка к нормальному закону распределения. В табл. 3 представлены численные значения остатков и их проценты отклонений. Временной график остатков (рис. 2) указывает на случайный характер изменения остатков от времени (последовательности) проведения опытов. Дальнейшее повышение точности модели не возможно. Анализ зависимости остатков от ŷ
(расчетного значения) показывает, что наибольшие разбросы остатков наблюдаются для X
4 = 0 кгс (y
= 32581...32730) и X
4 = 100 кгс (y
= 25124...25309). Наименьший разброс при X
4 = 40 кгс. Однако статистическая значимость такого заключения требует знания обоснованного значения дисперсии воспроизводимости.
. Она сравнительно близка к нормальному закону распределения. В табл. 3 представлены численные значения остатков и их проценты отклонений. Временной график остатков (рис. 2) указывает на случайный характер изменения остатков от времени (последовательности) проведения опытов. Дальнейшее повышение точности модели не возможно. Анализ зависимости остатков от ŷ
(расчетного значения) показывает, что наибольшие разбросы остатков наблюдаются для X
4 = 0 кгс (y
= 32581...32730) и X
4 = 100 кгс (y
= 25124...25309). Наименьший разброс при X
4 = 40 кгс. Однако статистическая значимость такого заключения требует знания обоснованного значения дисперсии воспроизводимости.

Рис. 2. Временной график остатков
Учет в математической модели разнообразных систематических погрешностей, нелинейностей, взаимодействий неуправляемых факторов позволил повысить точность средства измерения по критерию средней абсолютной погрешности аппроксимации до 0,012% – в 13,3 раза, а по критерию среднеквадратичной погрешности аппроксимации до 4,80 (табл. 1) – в 11,2 раза.
План эксперимента 2 2 //4 для средней абсолютной погрешности аппроксимации в % и полученные результаты при использованиии только средства измерения и средства измерения с математической моделью систематической погрешностей представлен в табл. 4.
Математическая модель для средней абсолютной погрешности аппроксимации, полученная по эксперименту 2 2 //4, со структурой модели (1) и результатам функционирования средства измерения без математической модели и с ее использованием, имеет вид
ŷ = 0,043 + 0,043x 1 ...0,037x 2 ...0,037x 1 x 2
где x 1 – ортогональный контраст фактора X 1 (СИ) – средство измерения;
x 2 – ортогональный контраст фактора X 2 (ММ) – математическая модель систематических погрешностей используемого средства измерения;
x 1 x 2 – взаимодействие факторов X 1 (СИ) и X 2 (ММ).
Таблица 3
Остатки и их проценты отклонений
1
– Номер опыта; 2
– Отклик по эксперименту; 3
– Отклик по модели; 4
– Остаток;
5
– Процент отклонения; 6
– Номер опыта; 7
– Отклик по эксперименту;
8
– Отклик по модели; 9
– Остаток; 10
– Процент отклонения
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 32581 | 32574,2 | 6,832 | 0,0210 | 55 | 32581 | 32576,6 | 4,431 | 0,0136 |
| 2 | 31115 | 31108,7 | 6,349 | 0,0204 | 56 | 31115 | 31111,1 | 3,948 | 0,0127 |
| 3 | 29635 | 29631,7 | 3,308 | 0,0112 | 57 | 29633 | 29634,1 | –1,092 | –0,0037 |
| 4 | 28144 | 28143,3 | 0,710 | 0,0025 | 58 | 28141 | 28145,7 | –4,691 | –0,0167 |
| 5 | 26640 | 26643,4 | –3,445 | –0,0129 | 59 | 26637 | 26645,8 | –8,846 | –0,0332 |
| 6 | 25128 | 25132,2 | –4,159 | –0,0165 | 60 | 25124 | 25134,6 | –10,559 | –0,0420 |
| 7 | 32625 | 32638,6 | –13,602 | –0,0417 | 61 | 32649 | 32641 | 7,997 | 0,0245 |
| 8 | 31175 | 31173,1 | 1,915 | 0,0061 | 62 | 31179 | 31175,5 | 3,514 | 0,0113 |
| 9 | 29694 | 29696,1 | –2,126 | –0,0072 | 63 | 29699 | 29698,5 | 0,473 | 0,0016 |
| 10 | 28208 | 28207,7 | 0,276 | 0,0010 | 64 | 28209 | 28210,1 | –1,125 | –0,0040 |
| 11 | 26709 | 26707,9 | 1,120 | 0,0042 | 65 | 26711 | 26710,3 | 0,719 | 0,0027 |
| 12 | 25198 | 25196,6 | 1,407 | 0,0056 | 66 | 25199 | 25199 | 0,006 | 0,0000 |
| 13 | 32659 | 32666,7 | –7,680 | –0,0235 | 67 | 32660 | 32669,1 | –9,081 | –0,0278 |
| 14 | 31199 | 31201,2 | –2,163 | –0,0069 | 68 | 31200 | 31203,6 | –3,564 | –0,0114 |
| 15 | 29723 | 29724,2 | –1,204 | –0,0040 | 69 | 29726 | 29726,6 | –0,605 | –0,0020 |
| 16 | 28241 | 28235,8 | 5,198 | 0,0184 | 70 | 28242 | 28238,2 | 3,797 | 0,0134 |
| 17 | 26741 | 26736 | 5,042 | 0,0189 | 71 | 26742 | 26738,4 | 3,642 | 0,0136 |
| 18 | 25232 | 25224,7 | 7,329 | 0,0290 | 72 | 25233 | 25227,1 | 5,928 | 0,0235 |
| 19 | 32632 | 32636,5 | –4,543 | –0,0139 | 73 | 32630 | 32637 | –7,012 | –0,0215 |
| 20 | 31175 | 31177,1 | –2,086 | –0,0067 | 74 | 31173 | 31177,6 | –4,554 | –0,0146 |
| 21 | 29705 | 29706,2 | –1,185 | –0,0040 | 75 | 29703 | 29706,7 | –3,654 | –0,0123 |
| 22 | 28225 | 28223,8 | 1,157 | 0,0041 | 76 | 28223 | 28224,3 | –1,311 | –0,0046 |
| 23 | 26734 | 26730,1 | 3,942 | 0,0147 | 77 | 26733 | 26730,5 | 2,474 | 0,0093 |
| 24 | 25233 | 25224,8 | 8,170 | 0,0324 | 78 | 25233 | 25225,3 | 7,702 | 0,0305 |
| 25 | 32710 | 32707,4 | 2,623 | 0,0080 | 79 | 32710 | 32707,8 | 2,155 | 0,0066 |
| 26 | 31251 | 31247,9 | 3,081 | 0,0099 | 80 | 31249 | 31248,4 | 0,612 | 0,0020 |
| 27 | 29777 | 29777 | –0,019 | –0,0001 | 81 | 29775 | 29777,5 | –2,488 | –0,0084 |
| 28 | 28294 | 28294,7 | –0,676 | –0,0024 | 82 | 28292 | 28295,1 | –3,145 | –0,0111 |
| 29 | 26799 | 26800,9 | –1,891 | –0,0071 | 83 | 26799 | 26801,4 | –2,360 | –0,0088 |
| 30 | 25297 | 25295,7 | 1,336 | 0,0053 | 84 | 25296 | 25296,1 | –0,132 | –0,0005 |
| 31 | 32730 | 32723,7 | 6,349 | 0,0194 | 85 | 32729 | 32724,1 | 4,880 | 0,0149 |
| 32 | 31269 | 31264,2 | 4,806 | 0,0154 | 86 | 31267 | 31264,7 | 2,338 | 0,0075 |
| 33 | 29794 | 29793,3 | 0,707 | 0,0024 | 87 | 29793 | 29793,8 | –0,762 | –0,0026 |
| 34 | 28310 | 28311 | –0,951 | –0,0034 | 88 | 28309 | 28311,4 | –2,419 | –0,0085 |
| 35 | 26814 | 26817,2 | –3,166 | –0,0118 | 89 | 26814 | 26817,6 | –3,634 | –0,0136 |
| 36 | 25309 | 25311,9 | –2,938 | –0,0116 | 90 | 25309 | 25312,4 | –3,407 | –0,0135 |
| 37 | 32616 | 32619,1 | –3,053 | –0,0094 | 91 | 32608 | 32616,2 | –8,183 | –0,0251 |
| 38 | 31152 | 31154,5 | –2,525 | –0,0081 | 92 | 31148 | 31151,7 | –3,656 | –0,0117 |
| 39 | 29677 | 29678,6 | –1,555 | –0,0052 | 93 | 29675 | 29675,7 | –0,686 | –0,0023 |
| 40 | 28192 | 28191,1 | 0,858 | 0,0030 | 94 | 28192 | 28188,3 | 3,727 | 0,0132 |
| 41 | 26696 | 26692,3 | 3,713 | 0,0139 | 95 | 26692 | 26689,4 | 2,582 | 0,0097 |
| 42 | 25189 | 25182 | 7,010 | 0,0278 | 96 | 25189 | 25179,1 | 9,880 | 0,0392 |
| 43 | 32713 | 32707,9 | 5,132 | 0,0157 | 97 | 32704 | 32705 | –0,998 | –0,0031 |
| 44 | 31244 | 31243,3 | 0,660 | 0,0021 | 98 | 31240 | 31240,5 | –0,471 | –0,0015 |
| 45 | 29770 | 29767,4 | 2,630 | 0,0088 | 99 | 29764 | 29764,5 | –0,501 | –0,0017 |
| 46 | 28285 | 28280 | 5,043 | 0,0178 | 100 | 28278 | 28277,1 | 0,912 | 0,0032 |
| 47 | 26784 | 26781,1 | 2,898 | 0,0108 | 101 | 26778 | 26778,2 | –0,233 | –0,0009 |
| 48 | 25262 | 25270,8 | –8,805 | –0,0349 | 102 | 25262 | 25267,9 | –5,935 | –0,0235 |
| 49 | 32717 | 32710,7 | 6,318 | 0,0193 | 103 | 32710 | 32707,8 | 2,187 | 0,0067 |
| 50 | 31249 | 31246,2 | 2,845 | 0,0091 | 104 | 31245 | 31243,3 | 1,715 | 0,0055 |
| 51 | 29770 | 29770,2 | –0,185 | –0,0006 | 105 | 29767 | 29767,3 | –0,315 | –0,0011 |
| 52 | 28280 | 28282,8 | –2,772 | –0,0098 | 106 | 28279 | 28279,9 | –0,903 | –0,0032 |
| 53 | 26779 | 26783,9 | –4,917 | –0,0184 | 107 | 26779 | 26781 | –2,048 | –0,0076 |
| 54 | 25267 | 25273,6 | –6,619 | –0,0262 | 108 | 25267 | 25270,8 | –3,750 | –0,0148 |
| Средняя абсолютная относительная погрешность в процентах – 0,0119. | |||||||||
Таблица 4
План эксперимента 2 2 //4
Анализ коэффициентов модели показывает, что фактор X 2 (ММ) уменьшает систематическую погрешность не только в виде главного эффекта x 2 (коэффициент b 2 = –0,037), но и за счет взаимодействия (эмергентности) факторов X 1 (СИ) · X 2 (ММ) (коэффициент b 12 = –0,037).
Аналогичную модель можно получить и для критерия среднеквадратичной погрешности аппроксимации.
Для фактической реализации полученной модели (2) необходимо измерить и использовать информацию о температуре окружающей среды и напряжении питания с помощью датчиков и провести расчет результата с применением микропроцессора.
Результаты математического моделирования шестикомпонентных тензометрических измерительных систем
В рассмотрено математическое моделирование шестикомпонентных тензометрических измерительных систем. Предложенный метод был внедрен на Киевском механическом заводе (ныне Авиационный научно-технический комплекс им. О.К. Антонова). Впервые в практике проведения аналогичных измерений этот метод в значительной степени позволил исключить последствия физических несовершенств измерительных систем, проявляющихся в виде взаимодействия между каналами, влияния других каналов на рассматриваемый канал, нелинейностей и изучить структурные взаимосвязи различных каналов.
Использование метода математического моделирования в реальных условиях предприятия показало, что время проведения опытов сокращается в 10...15 раз; существенно (до 60 раз) повышается эффективность обработки измерительной информации; в 2...3 раза сокращается количество исполнителей, занятых в измерительных экспериментах.
Итоговый вывод о целесообразности использования изложенного подхода зависит от экономической эффективности следующих сравниваемых вариантов.
Высокоточного средства измерения и, следовательно, более дорогого, используемого в нормированных (стандартных) условиях, которые необходимо создать и поддерживать.
Средства измерения менее высокой точности, используемого в не нормированных (не стандартных) условиях с применением полученной математической модели.
Основные выводы
1) Успешно реализованный системный подход в математическом моделировании средства измерения позволил учесть влияние факторов внешней – температура окружающей среды – и внутренней среды – напряжение питания. Эффективность извлечения полезной информации из исходных данных составила 100%.
2) В полученной многофакторной математической модели, структура которой априори исследователю не была известна, в удобной для интерпретации в предметной области форме раскрыты нелинейность средства измерения и системное влияние факторов (эмергентность) внешней и внутренней среды. В реальных условиях эксплуатации стабилизация этих факторов с необходимой точностью не представляется возможной.
3) Учет математической модели систематических погрешностей позволил повысить точность измерений по критерию средней абсолютной погрешности в 13,3 раза и по критерию среднеквадратичной погрешности в 11,2 раза.
Наши предложения
Лаборатория экспериментально-статистических методов и исследований готова предоставить алгоритмическое, программное обеспечение для получения многофакторных математических моделей, их анализа и интерпретации и передать накопленный опыт для использования при решении конкретных производственных и научных задач.
Мы готовы решить Ваши проблемы в указанных и многих других областях путем использования созданных за многие годы алгоритмов, программного обеспечения, ноу-хау; учебы и передачи опыта Вашим специалистам.
Литература:
- Рыбаков И.Н. Основы точности и метрологического обеспечения радиоэлектронных измерений. – М.: Изд-во стандартов, 1990. – 180 с.
- Радченко С.Г. Математическое моделирование технологических процессов в машиностроении.– К.: ЗАО «Укрспецмонтажпроект», 1998. – 274 с.
- Алимов Ю.И., Шаевич А.Б. Методологические особенности оценивания результатов количественного химического анализа // Журнал аналитической химии. – 1988. – Вып. 10. – Т. XLIII. – С. 1893...1916.
- Планирование, регрессия и анализ моделей PRIAM (ПРИАМ). SCMC–90; 325, 660, 668 // Каталог. Программные продукты Украины. Catalog. Software of Ukraine. – К.: СП «Текнор». – 1993. – C. 24...27.
- Зинченко В.П., Радченко С.Г. Метод моделирования многокомпонентных тензометрических измерительных систем. – К.: 1993. – 17 с. (Препр. / АН Украины. Ин-т кибернетики им. В.М.Глушкова; 93...31).
Быстрые флуктуации ε (t) определяют случайную погрешность, которую приближенно описывают эргодическим случайным процессом с нулевым математическим ожиданием. При проведении измерений с многократными наблюдениями эта составляющая проявляется в виде случайной величины, принимающей значения εi= ε (t i), взятые в моменты t i (i = 1,2,...,п) проведения наблюдений. Наиболее полной характеристикой случайной погрешности являются функции распределения. По известной дифференциальной функции распределения (плотности вероятности) ρ(ε) можно определить вероятность пребывания случайной погрешности в заданных
границах от ∆ н до ∆ в:
Так как ε = х - X , где X - истинное, ах- измеренное значение измеряемой величины, то Р∆ = Р{х - ∆ вн < X < х + ∆ вн } (∆ вн - симметричные границы интервала). Следовательно, вероятность Р∆ соответствует вероятности пребывания истинного значения на интервале от х - ∆ вн до х + ∆ вн. Поскольку общая погрешность ∆ = Θ + ε, то ее плотность вероятности можно определить, сместив график ρ(ε) на Θ. В данном случае нижнюю ∆ н и верхнюю ∆ в границы интервала, в котором с вероятностью Р∆ лежит погрешность, выбирают симметрично относительно математического ожидания, поэтому I∆ Н I≠ ∆ е
4.10.4. Примеры законов распределения погрешностей
Для анализа результата измерений необходимо знать законы распределения отдельных составляющих погрешности, по которым можно определить закон распределения общей погрешности и решить вопрос о вычислении границ погрешностей. В некоторых случаях удается оценить законы распределения составляющих погрешности до проведения опыта на основе анализа причин их возникновения.
Равномерный закон. Этому закону подчинены погрешности, возникающие при квантовании и дискретизации сигнала. Например, при измерении постоянного напряжения U x путем его сравнения с образцовым напряжением, изменяющимся по ступенчатому закону с постоянным шагом Uст, результат измерений определяется числом n ступенек, зафиксированным с помощью электронного счетчика, и погрешностью квантования ∆U кв: U x = nUст - ∆U KB . Поскольку значение измеряемого напряжения неизвестно и нельзя указать область его предпочтительных значений, погрешность квантования считают распределенной по равномерному закону от 0 до Uст. Систематическая погрешность
График плотности вероятности случайной погрешности ε = ∆U кв – Θ получается смещением графика ρ(U KB) на Uct/2. Предельная погрешность ∆п = Uct /2. СКО случайной погрешности
Для погрешностей, о которых ничего не известно, кроме их пределов, равномерный закон является удобной математической моделью, как дающий наибольшую погрешность измерений. Например, при анализе неисключенной систематической погрешности удается оценить лишь ее предельные значения ±Θ н. Закон распределения неисключеннойсистематической погрешности моделируют равномерным законом с СКО σ = Θ/√12. Согласно ГОСТ 8.009-84 равномерно распределенной считают погрешность из-за вариациипоказаний в пределах +Н/2с СКО σ =H√ 12 , где Н =IС б -С м I.
Например, при измерении временного интервала цифровым методом, если начало измеряемого интервала не синхронизировано с последовательностью счетных импульсов, результат измерений T x =nT 0 -∆t H +∆t k =nT 0 -∆t д, где ∆t н и ∆t K погрешности дискретизации в начале и конце интервала Т х, ∆t д общая погрешность дискретизации. Погрешности ∆t н и ∆t K подчинены равномерному закону с предельными значениями 0 и Т 0 . Если интервал Т х не измерен, то случайные погрешности независимы, а закон распределения общей погрешности дискретизации ∆t д треугольный с предельными значениями ±Т 0 .
Характеристики окружающей среды, в которой проводятся измерения, называют условиями измерений. Это климатические условия (температура, относительная влажность воздуха, атмосферное давление), электрические и магнитные поля, механические и акустические факторы (вибрации, ударные нагрузки, сотрясения), ионизирующие излучения, газовый состав атмосферы и т.п. Так как они оказывают влияние на результат измерений, то для средств измерения в нормативно-технической документации всегда указываются условия, в которых нормированы их метрологические характеристики.
Метрологические характеристики средств измерений нормируют раздельно для нормальных и рабочих условий применения.
4.12. Организация измерительного эксперимента
Измерение выполняется оптимально, если результат и желаемая точность достигнуты самыми простыми средствами и в соответствии с простейшей стратегией.
Подготовка включает уточнение задачи измерений, планирование измерительного эксперимента, выбор требуемых методов и технических средств, в том числе и вспомогательное оборудование (источники питания, соединение с измеряемой средой, средства сопряжения, средства подвода охладителя, если требуется и т.д.); калибровку механических и юстировку оптических приборов, градуировку электронных средств.
В общем виде модель погрешности 0,95(t) может быть представлена в виде 0,95(t) = 0 + F(t), где D0 -- начальная погрешность СИ; F(t) -- случайная для совокупности СИ данного типа функция времени, обусловленная физико-химическими процессами постепенного износа и старения элементов и блоков. Получить точное выражение для функции F(t) исходя из физических моделей процессов старения практически не представляется возможным. Поэтому, основываясь на данных экспериментальных исследований изменения погрешностей во времени, функцию F(t) аппроксимируют той или иной математической зависимостью.
Простейшей моделью изменения погрешности является линейная:
где v скорость изменения погрешности. Как показали проведенные исследования, данная модель удовлетворительно описывает старение СИ в возрасте от одного до пяти лет. Использование ее в других диапазонах времени невозможно ввиду явного противоречия между определенными по этой формуле и экспериментальными значениями частоты отказов.
Метрологические отказы возникают периодически. Механизм их периодичности иллюстрирует рис.1, а, где прямой линией 1 показано изменение 95%-ного квантиля при линейном законе.

Рис. 2.
При метрологическом отказе погрешность D0,95(t) превышает значение Dпр=D0+nD3, где D3 -- значение запаса нормируемого предела погрешности, необходимого для обеспечения долговременной работоспособности СИ. При каждом таком отказе производится ремонт прибора и его погрешность возвращается к исходному значению D0. По прошествии времени Тр= ti - ti-1 опять происходит отказ (моменты tt, t2, t3 и т.д.), после которого вновь производится ремонт. Следовательно, процесс изменения погрешности СИ описывается ломаной линией 2 на рис.1, а, которая может быть представлена уравнением

где n -- число отказов (или ремонтов) СИ. Если число отказов считать целым, то это уравнение описывает дискретные точки на прямой 1 (рис.2, а). Если же условно принять, что п может принимать и дробные значения, то формула (2) будет описывать всю прямую 1 изменения погрешности D0,95(t) при отсутствии отказов.
Частота метрологических отказов увеличивается с ростом скорости v. Она столь же сильно зависит от запаса нормируемого значения погрешности D3 по отношению к фактическому значению погрешности средства измерений D0 на момент изготовления или окончания ремонта прибора. Практические возможности воздействия на скорость изменения v и запас погрешности D3 совершенно различны. Скорость старения определяется существующей технологией производства. Запас погрешности для первого межремонтного интервала определяется решениями, принятыми производителем СИ, а для всех последующих межремонтных интервалов -- уровнем культуры ремонтной службы пользователя.
Если метрологическая служба предприятия обеспечивает при ремонте погрешность СИ, равную погрешности D0 на момент изготовления, то частота метрологических отказов будет малой. Если же при ремонте лишь обеспечивается выполнение условия D0 (0,9... 0,95) Dпр, то погрешность может выйти за пределы допустимых значений уже в ближайшие месяцы эксплуатации СИ и большую часть межповерочного интервала оно будет эксплуатироваться с погрешностью, превышающей его класс точности. Поэтому основным практическим средством достижения долговременной метрологической исправности средства измерений является обеспечение достаточно большого запаса D3, нормируемого по отношению к пределу Dпр.
Постепенное непрерывное расходование этого запаса обеспечивает на некоторый определенный период времени метрологически исправное состояние СИ. Ведущие приборостроительные заводы обеспечивают D3 = (0,4...0,5) Dпр, что при средней скорости старения v = = 0,05АП /год позволяет получать межремонтный интервал Тр= D3 = 1/Т/v = 8... 10 лет и частоту отказов р= 0,1... 0,125 год-1.
При изменении погрешности СИ в соответствии с формулой (1) все межремонтные интервалы Тр = 1/Т будут равны между собой, а частота метрологических отказов р будет постоянной в течение всего срока эксплуатации. Однако проведенные экспериментальные исследования показали, что на практике это не выполняется.
В общем случае результаты измерений и их погрешности должны рассматриваться как функции, изменяющиеся во времени случайным образом, т.е. случайные функции, или, как принято говорить в математике, случайные процессы. Поэтому математическое описание результатов и погрешностей измерений (т.е. их математические модели) должно строиться на основе теории случайных процессов. Изложим основные моменты теории случайных функций.
Случайным процессом X(t) называется процесс (функция), значение которого при любом фиксированном значении t = tQ является случайной величиной X(t ). Конкретный вид процесса (функции), полученный в результате опыта, называется реализацией .
Рис. 4. Вид случайных функций
Каждая реализация является неслучайной функцией времени. Семейство реализаций при каком-либо фиксированном значении времени t (рис. 4) представляет собой случайную величину, называемую сечением случайной функции, соответствующим моменту времени t . Следовательно, случайная функция совмещает в себе характерные признаки случайной величины и детерминированной функции. При фиксированном значении аргумента она превращается в случайную величину, а в результате каждого отдельного опыта становится детерминированной функцией.
Математическим ожиданием случайной функции X(t) называется неслучайная функция которая при каждом значении аргумента t равна математическому ожиданию соответствующего сечения:
где p(x, t) - одномерная плотность распределения случайной величины х в соответствующем сечении случайного процесса X(t).
Дисперсией случайной функции X(t) называется неслучайная функция значение которой для каждого момента времени равно дисперсии соответствующего сечения, т.е. дисперсия характеризует разброс реализаций относительно m (t).
Корреляционная функция - неслучайная функция R(t, t") двух аргументов t и t", которая при каждой паре значений аргументов равна ковариации соответствующих сечений случайного процесса:
Корреляционная функция, называемая иногда автокорреляционной, описывает статистическую связь между мгновенными значениями случайной функции, разделенными заданным значением времени т = t"-t. При равенстве аргументов корреляционная функция равна дисперсии случайного процесса. Она всегда неотрицательна.
Случайные процессы, протекающие во времени однородно, частные реализации которых с постоянной амплитудой колеблются вокруг средней функции, называются стационарными . Количественно свойства стационарных процессов характеризуются следующими условиями:
Математическое ожидание постоянно;
Дисперсия по сечениям является постоянной величиной;
Корреляционная функция зависит не от значения аргументов, а только от промежутка.
Важной характеристикой стационарного случайного процесса является его спектральная плотность S(w), которая описывает частотный состав случайного процесса при w>О и выражает среднюю мощность случайного процесса, приходящуюся на единицу полосы частот:
Спектральная плотность стационарного случайного процесса является неотрицательной функцией частоты. Корреляционная функция может быть выражена через спектральную плотность
При построении математической модели погрешности измерений следует учитывать всю информацию о проводимом измерении и его элементах.
Каждая из них может быть обусловлена действием нескольких различных источников погрешностей и в свою очередь состоять также из некоторого числа составляющих.
Для описания погрешностей используются теория вероятностей и математическая статистика, однако прежде необходимо сделать ряд существенных оговорок:
Применение методов математической статистики к обработке результатов измерений правомочно лишь в предположении о независимости между собой отдельных получаемых отсчетов;
Большинство используемых в метрологии формул теории вероятностей правомерны только для непрерывных распределений, в то время как распределения погрешностей вследствие неизбежного квантования отсчетов, строго говоря, всегда дискретны, т.е. погрешность может принимать лишь счетное множество значений.
Таким образом, условия непрерывности и независимости для результатов измерений и их погрешностей соблюдаются приближенно, а иногда и не соблюдаются. В математике под термином "непрерывная случайная величина" понимается существенно более узкое, ограниченное рядом условий понятие, чем "случайная погрешность" в метрологии.
В метрологии принято различать три группы характеристик и параметров погрешностей. Первая группа-задаваемые в качестве требуемых или допускаемых нормы характеристик погрешности измерений (нормы погрешностей). Вторая группа характеристик- погрешности, приписываемые совокупности выполняемых по определенной методике измерений. Характеристики этих двух групп применяются в основном при массовых технических измерениях и представляют собой вероятностные характеристики погрешности измерений. Третья группа характеристик-статистические оценки погрешностей измерений отражают близость отдельного, экспериментально полученного результата измерения к истинному значению измеряемой величины. Они используются в случае измерений, проводимых при научных исследованиях и метрологических работах.
Совокупность формул, описывающих состояние, движение и взаимодействие объектов, полученных в рамках выбранных физических моделей на основе законов физики, будем называть математической моделью объекта или процесса . Процесс создания математической модели можно разделить на ряд этапов:
1) составление формул и уравнений, описывающих состояние, движение и взаимодействие объектов в рамках построенной физической модели. Этап включает запись в математических терминах сформулированных свойств объектов, процессов и связей между ними;
2) исследование математических задач, к которым приходят на первом этапе. Основным вопросом здесь является решение прямой задачи, т.е. получение численных данных и теоретических следствий. На этом этапе важную роль приобретают математический аппарат и вычислительная техника (компьютер).
3) выяснение того, согласуются ли результаты анализа и вычислений или следствия из них с результатами наблюдений в пределах точности последних, т.е. удовлетворяет ли принятая физическая и (или) математическая модель практике-основному критерию истинности наших представлений об окружающем мире.
Отклонение результатов расчетов от результатов наблюдений свидетельствует либо о неправильности применяемых математических методов анализа и расчета, либо о неверности принятой физической модели. Выяснение источников ошибок требует большого искусства и высокой квалификации исследователя.
Часто при построении математической модели некоторые ее характеристики или связи между параметрами остаются неопределенными вследствие ограниченности наших знаний о физических свойствах объекта. Например, оказывается, что число уравнений, описывающих физические свойства объекта или процесса и связи между объектами, меньше числа физических параметров, характеризующих объект. В этих случаях приходится вводить дополнительные соотношения, характеризующие объект исследования и его свойства, иногда даже пытаться угадать эти свойства, для того, чтобы задача могла быть решена и результаты соответствовали результатам опыта в пределах заданной погрешности.
4.3.1. Линейная модель изменения погрешности
В общем виде модель погрешности Л О95 (0 может быть представлена в виде A ogs (t) = А 0 + F{t), где Д 0 - начальная погрешность СИ; F(t) - случайная для совокупности СИ данного типа функция времени, обусловленная физико-химическими процессами постепенного износа и старения элементов и блоков. Получить точное выражение для функции F(t) исходя из физических моделей процессов старения практически не представляется возможным. Поэтому, основываясь на данных экспериментальных исследований изменения погрешностей во времени, функцию F(t) аппроксимируют той или иной математической зависимостью.
Простейшей моделью изменения погрешности является линейная;
\ И (Г) = Д 0 + vt, (4.1)
где v - скорость изменения погрешности. Как показали проведенные исследования , данная модель удовлетворительно описывает старение СИ в возрасте от одного до пяти лет. Использование ее в других диапазонах времени невозможно ввиду явного противоречия между определенными по этой формуле и экспериментальными значениями частоты отказов.
Метрологические отказы возникают периодически. Механизм их периодичности иллюстрирует рис. 4.2,а, где прямой линией 1 показано изменение 95%-ного квантиля при линейном законе.
| 1 | ||
| 1 | ||
| .......... А | ||
| // | 1-2 | |
| В) |
Рис. 4.2. Линейный (а) и экспоненциальный {б, в) законы изменения
погрешности
При метрологическом отказе погрешность Д 0 95 (0 превышает значение Д пр = Д 0 + Д з, где Д з - значение запаса нормируемого предела погрешности, необходимого для обеспечения долговременной работоспособности СИ. При каждом таком отказе производится ремонт прибора, и его погрешность возвращается к исходному значению Д 0 . По прошествии времени Т = А - t ; опять происходит отказ (моменты t v t 2 , t 3 и т.д.), после которого вновь производится ремонт. Следовательно, процесс изменения погрешности СИ описывается ломаной линией 2 на рис. 4.2, а, которая может быть представлена уравнением
д 095 (0 = Д 0 + п Д, (4.2)
где п - число отказов (или ремонтов) СИ. Если число отказов считать целым числом, то это уравнение описывает дискретные точки на прямой 1 (рис. 4.2,а). Если условно принять, что я может принимать и дробные значения, то формула (4.2) будет описывать всю прямую 1 изменения погрешности Д 095 (0 при отсутствии отказов.
Частота метрологических отказов увеличивается с ростом скорости v. Она столь же сильно зависит от запаса нормируемого значения погрешности Д з по отношению к фактическому значению погрешности средства измерений Д 0 на момент изготовления или окончания ремонта прибора. Практические возможности воздействия на скорость изменения v и запас погрешности Д з совершенно различны. Скорость старения определяется существующей технологией производства. Запас погрешности для первого межремонтного интервала определяется решениями, принятыми производителем СИ, а для всех последующих межремонтных интервалов - уровнем культуры ремонтной службы пользователя.
Если метрологическая служба предприятия обеспечивает при ремонте погрешность СИ, равную погрешности Д 0 на момент изготовления, то частота метрологических отказов будет малой. Если же при ремонте лишь обеспечивается выполнение условия Д 0 = (0,9,...,0,95) Д пр, то погрешность может выйти за пределы допустимых значений уже в ближайшие месяцы эксплуатации СИ и большую часть межповерочного интервала оно будет эксплуатироваться с погрешностью, превышающей его класс точности. Поэтому основным практическим средством достижения долговременной метрологической исправности средства измерений является обеспечение достаточно большого запаса Д з, нормируемого по отношению к пределу Д пр.
Постепенное непрерывное расходование этого запаса обеспечивает на некоторый определенный период времени метрологически исправное состояние СИ. Ведущие приборостроительные заводы обеспечивают Д з = (0,4,...,0,5) Л пр, что при средней скорости старения v = 0,05 Л пр в год позволяет получать межремонтный интервал Т = Д/v = 8,...,10 лет и частоту отказов ю = 1/71 - 0,1,..., 0,125 год 1 .
При изменении погрешности СИ в соответствии с формулой (4.1) все межремонтные интервалы Т будут равны между собой, а частота метрологических отказов ю = \/Тбудет постоянной в течение всего срока эксплуатации.
4.3.2. Экспоненциальная модель изменения погрешности
В реальности для одних приборов межремонтные интервалы уменьшаются, для других - увеличиваются. Это может быть объяснено тем, что погрешность СИ с течением времени экспоненциально возрастает или убывает. При ускоряющемся возрастании погрешности (рис. 4.2,6) каждый последующий межремонтный интервал короче предыдущего и частота метрологических отказов а>(0 с течением времени возрастает. При замедленном возрастании погрешности (рис. 4.2,в) каждый последующий межремонтный интервал длиннее предыдущего и частота метрологических отказов со(0 с течением времени убывает вплоть до нуля.
Для рассмотренных случаев изменения погрешности во времени описываются на основе экспоненциальной модели. В ней частота метрологических отказов «
ш(0 = w 0 e"", (4.3)
где (о 0 - частота метрологических отказов на момент изготовления средства измерений (т. е. при t = 0), год "; а - положительное или отрицательное ускорение процесса метрологического старения, год 1 .
Число отказов n(t) определяется через частоту отказов а>(0 и при ее экспоненциальном изменении, согласно формуле (4.3), рассчитывается как
л(г) = /(o(T)rfr = \^e at dx = -1).
Тогда изменение во времени погрешности СИ с учетом формулы (4.2) имеет вид
Д 0 95 (0 = Д 0 + Я(0Д 3 = д 0 + (4.4)
Указанная зависимость показана кривыми 1 на рис. 4.2,6 и 4.2,в.
Раздел I. МЕТРОЛОГИЯ
Практическое использование формулы (4.4) требует знания четырех параметров: начального значения погрешности (Д 0), абсолютного запаса погрешности (Д 3), начальной частоты метрологических отказов (со 0) при t= 0 и ускорения (а) процесса старения. Уравнения для определения названных параметров, получаемые из уравнения (4.4), оказываются трансцендентными, что существенно затрудняет их применение.
С целью упрощения использования уравнения (4.4) необходимо разложить в ряд экспоненциальную функцию и взять три первых члена этого разложения. В результате зависимость погрешности СИ от времени будет представлена в виде
А о,95^ = А 0 + A 3°V + Аз»о^/2 = \ + vt + af/2, (4.5)
где v - начальная скорость возрастания погрешности, %; а А - абсолютное значение ускорения изменения погрешности, %. В частном случае, когда а = 0, (4.5) превращается в линейное уравнение вида (4.1).
Срок службы СИ - это календарное время, прошедшее с момента его изготовления до конца эксплуатации. При положительном ускорении процесса старения (см. рис. 4.2,6) частота отказов с увеличением срока службы возрастает и по истечении времени Г сл его приходится настолько часто ремонтировать, что эксплуатация становится экономически невыгодной, так как дешевле купить новый прибор. Экономическая целесообразность ремонта определяется отношением средней стоимости одного ремонта с р к стоимости с к нового средства измерений, названного в относительной глубиной ремонта с = с р /с к. Срок службы СИ
Глава 4. Метрологическая надежность средств измерений
Решая полученное уравнение совместно с первым выражением из (4.6), можно рассчитать общее число отказов (ремонтов) СИ в течение срока эксплуатации.
Пример 4.1. Для электромеханических измерительных приборов магнитоэлектрической системы класса точности 0,5 глубина ремонта составляет с = 0,3... 0,4; частота метрологических отказов на момент изготовления ш 0 = 0,11 год 1 , ускорение процесса старения а ~ 0,19 год 1 . Определите срок службы таких приборов и общее число отказов.
Срок службы прибора рассчитывается по формуле (4.7):
Т сд = ]/ Дз-ОД 1-0,19 = 12,63 года.
Уравнение для расчета общего числа отказов имеет вид
п ъ = - [ехр(я/ д/а с ■ (0 0)-1],
Подставив в него числовые данные, получим
4 = ^19 1? хр (0 " 19 /^ 0 " 19 "°" 3 " 0,1 1)~*]= 0,579(е 5 " 8 -l)=5,8.
Данные расчета соответствуют экспериментальным данным, согласно которым средний срок службы рассматриваемых приборов составляет 11-12 лет, в течение которых они имеют по 4-6 ремонтов.
При отрицательном ускорении процесса старения СИ межремонтный период увеличивается. После некоторого числа ремонтов n L он становится бесконечным, метрологические отказы не возникают и СИ работает до тех пор, пока морально не устареет. В этом случае (а < 0) число метрологических отказов
% = = lim n(t) = lim^ (e al -1) = ^ . (->■» (->■» a a.
Погрешность СИ стремится к пределу, равному, согласно (4.4),
Д 0 95 (оо) = д 0 - -S- А 3 = ДО + „_ д. (4.8)
Экспоненциальная модель процесса старения позволяет описать изменения пофешности СИ при увеличении его возраста от года и практически до бесконечности. Однако данная модель имеет ряд недостатков. Для СИ с отрицательным ускорением процесса старения она прогнозирует при t-> °° стремление пофешности к предельному
значению (4.8). В то же время для СИ с положительным ускорением модель прогнозирует неограниченное возрастание погрешности с течением времени, что противоречит практике.
Некоторые недостатки экспоненциальной модели старения удается устранить при использовании так называемой логистической модели, а также полиномиальными и диффузионными марковскими моделями или моделями на основе процессов авторегрессии проинтегрированного скользящего среднего .
В технике используется большое число показателей надежности, которые приведены в стандарте ГОСТ 27.002-89. Основные из них находят применение и в теории метрологической надежности. Знание показателей метрологической надежности позволяет потребителю оптимально использовать СИ, планировать мощности ремонтных участков, размер резервного фонда приборов, обоснованно назначать межповерочные интервалы и проводить мероприятия по техническому обслуживанию и ремонту СИ.
Метрологические отказы при эксплуатации СИ составляют более 60% на третьем году эксплуатации и достигают 96% при работе более четырех лет.
В качестве показателей ремонтопригодности используются вероятность и среднее время восстановления работоспособности СИ. Вероятностью восстановления работоспособного состояния называется вероятность того, что время восстановления работоспособного состояния СИ не превысит заданное значение. Она представляет собой значение функции распределения времени восстановления при /= где - заданное время восстановления. Средним временем восстановления работоспособного состояния называется математическое ожидание времени восстановления, определяемое до его функции распределения.
Похожие статьи